Calculating the Distance to Nearby Stars: The Stellar Parallax

Understanding Earth’s place in the universe has been a question in the minds of humans for millennia. From the first applications of astronomical trigonometry in Babylon, Egypt, Greece, or ancient Islam, to the precise astrophysical calculations used by astronomers in modern-day society — the human race has unremittingly pursued our cosmic address.
Trigonometry, the study of relationships between side lengths and angles of triangles, is a branch of mathematics dating as far back as 5,000 years ago. Largely regarded as an unremarkable subject of math today, trigonometry once revolutionized our species’ scientific capabilities, and unknown to most, continues to do so.
The trigonometric parallax is a method to discern a star’s distance from Earth. Parallax refers to the apparent change in the position of a given object depending on the observer’s line of sight, with respect to more distant “stationary” objects. When you hold your thumb out in front of your face and alternate opening and closing each eye, the position of your thumb moves, while the background appears to stay fixed. The distance your thumb appears to move is directly related to how far apart your eyes are.
The same principle can be applied to astronomical bodies. We may use trigonometric functions to calculate the distance of relatively close stars, using more distant stars as a fixed background. Any stars farther than ~100 parsecs (326 LY) have parallax angles too small to measure from the surface of the Earth with this technique. This is due to atmospheric interference. However, distances to stars closer than 100 parsecs can be calculated with ground-based telescopes. Using observations of a star six months apart, we may find the parallax angle. Because we know the distance between the Earth and the Sun (1 AU or ~93 million miles), and the angle of the given star relative to straight up, we may use the tangent function to calculate the distance (tan = opp/adj).
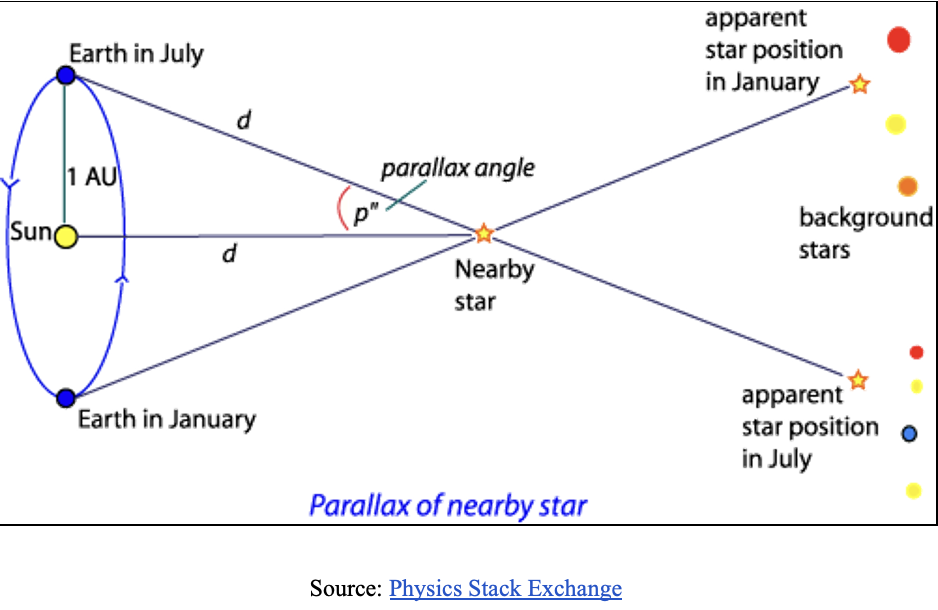
In the image above, it can be seen that: tan (p) = 1 AU / d. In this case, the opposite side from (p) is 1 AU and the adjacent side from (p) is the d — the distance to the nearby star. This can then be used to calculate the distance: d = 1 AU / tan (p).
Trigonometric parallaxes are measured in units of arcsecs and parsecs. This is because the degree to which stars are shifted is incredibly small. One arcsec is 1/3600 degrees. And one parsec is the distance of a star that has a parallax angle of one arcsec, hence the name “parsec.” To find the actual distance of one parsec we may use the formula above.
d = 1 AU / tan (1 arcsec)
d = 92,955,807.3 miles / tan (1/3600 degrees) = 19,173,511,582,127 mi * 1LY/5.88 trillion miles = 3.26 LY.
d = 1AU / tan (1/3600 degrees) = 206,265 AU * 1LY/63,115 AU = 3.26 LY
Thus, 1 parsec = 206,265 AU = 3.26 LY
The closest star to Earth is Proxima Centauri and has a parallax angle of 0.76813 arcsecs (the smaller the parallax angle the farther the star — a smaller shift means a greater distance). 0.76813 arcsecs * 1 degree/3600 arcsecs = 0.0002133694 degrees. We can use this to find the distance to the star.

d = 1AU / tan (0.0002133694 degrees) = 268,528.56835524 AU * 1 parsec/206,265 AU = 1.3 parsecs
1.3 parsecs * 3.26LY/1parsec = 4.2 LY.
Therefore, Proxima Centauri is 1.3 parsecs or 4.2 LY away.
A simpler way to do this does not involve the tangent function at all but relies on the relationships between the units: d = 1/p. The distance between the Earth and a nearby star is equal to 1AU divided by the parallax angle. This equation will result in an answer already in parsecs because one parsec is the distance of a star that has a parallax angle of one arc second (1/3600 degrees) using a baseline of 1 AU.
Using Proxima Centurai as an example:
d = 1AU/0.76813 arcsecs = 1.3 parsecs.
Trigonometry reveals the beauty and divine precision in mathematics and the fundamental structure of our reality. Trigonometric ratios and equations that remain true in every circumstance are the very laws of the universe, and they can be used to understand Earth’s place in relation to other astronomical bodies. These are the questions that define human curiosity, and with the application of trigonometry, we may begin to unravel the mysteries of the cosmos.
References
https://www.astronomynotes.com/starprop/s2.htm
https://astronomy.swin.edu.au/cosmos/t/trigonometric+parallax
https://www.teachastronomy.com/textbook/Properties-of-Stars/Stellar-Parallax/
https://physics.stackexchange.com/questions/286309/how-is-the-parallax-angle-actually-measured




